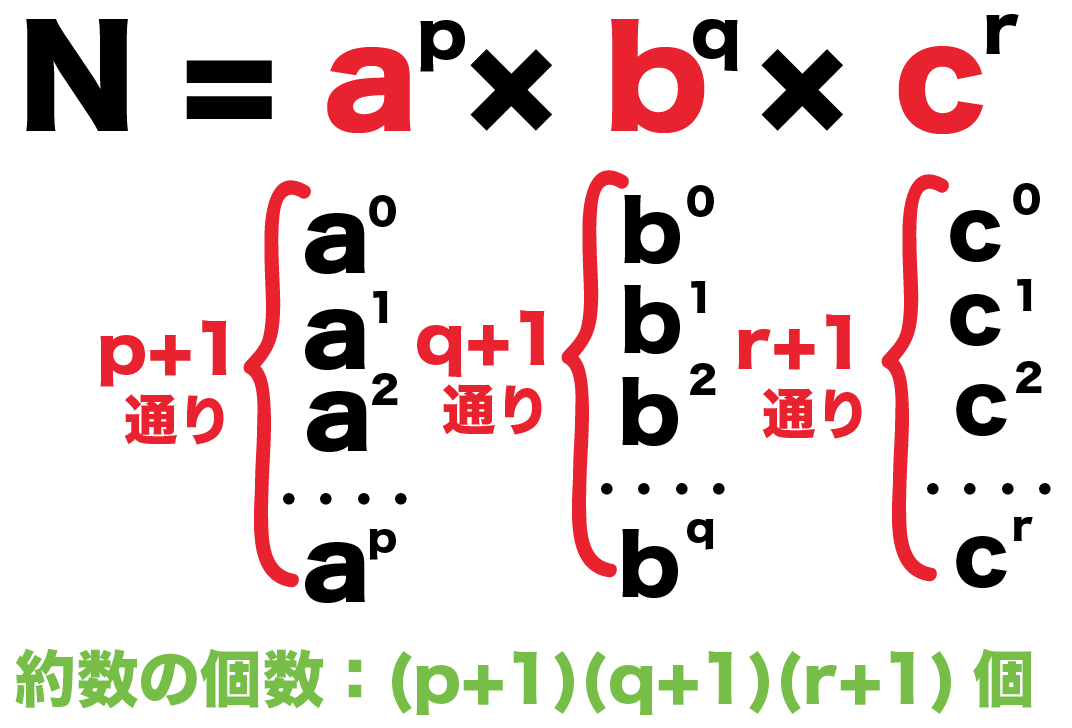ニュース 120の正の約数は何個あるか?. トピックに関する記事 – 120の正の約数は何個ありますか?
よって、120の約数は1 , 2 , 3 , 4 , 5 , 6 , 8 , 10 , 12 , 15 , 20 , 24 , 30 , 40 , 60 , 120 であることがわかります。 2つ以上の数に共通する約数を公約数といいます。12 の正の約数は,1, 2, 3, 4, 6, 12 である。 12 の正の倍数で 50 以下であるものは,12, 24, 36, 48 である。 (教科書 p.63) 123 は,1 + 2 + 3 = 6 より,3 の倍数である。 また,124 は,1 + 2 + 4 = 7 より,3 の倍数で はない。「1とかけ算して24になるのは24、2とかけ算して24になるのは……」と順に考えていくと、「1×24」「2×12」「3×8」「4×6」が見つかるね。 これらの数字がすべて24の約数になる んだ。 「4×6」 の後を考えると 「6×4」 が出てくるけど、これは「4×6」と同じこと。
120は偶数ですか?小さい順から十進表記で、6, 10, 14, 18, 22, 26, 30…と続く。 十進法では、−82, −38, 6, 10, 22, 54, 90, 138 などが単偶数で、−40, −16, 8, 12, 28, 64, 120 などが複偶数である。
約数の個数一覧は?
約数の個数
| 個数 | 数 |
|---|---|
| 1 | 1 |
| 2 | 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, … |
| 3 | 4, 9, 25, 49, 121, 169, 289, 361, 529, 841, … |
| 4 | 6, 8, 10, 14, 15, 21, 22, 26, 27, 33, 34, 35, … |
48,72 の共通因数は1,2,3,4,6,8,12,24 1 , 2 , 3 , 4 , 6 , 8 , 12 , 24 です。 数因子1,2,3,4,6,8,12,24 1 , 2 , 3 , 4 , 6 , 8 , 12 , 24 の最大公約数(最高公約数)は24 です。
96の正の約数は何個ありますか?
性質 96 は合成数であり、正の約数は 1, 2, 3, 4, 6, 8, 12, 16, 24, 32, 48, 96 である。 約数の和は252。
180は合成数であり、約数は1, 2, 3, 4, 5, 6, 9, 10, 12, 15, 18, 20, 30, 36, 45, 60, 90 と 180 である。 約数の和は546。
1260正の約数の個数はいくつですか?
16番目の高度合成数であり、約数を36個持つ。ここでふと疑問なのが、0は偶数なのか?ということです。 2で割り切れる数を偶数だと考えると、0はどっち? 気になって調べてみると、結論から先に言えば、0は偶数だそうです。ぐう‐すう【偶数】 2で割り切れる整数。 2、4、6、8など。
約数の「個数」を計算する!
「約数」 は、簡単にいうと 「割り切れる整数」 のことだったね。 今回は、 「約数の個数」 を求める方法について学習しよう。 例えば「12の約数」だったら、「1,2,3,4,6,12」だから、個数は 6個 というわけだよ。
100の約数はいくつですか?なので、100の約数は 1 , 2 , 4 , 5 , 10 , 20 , 25 , 50 , 100 です。 いかがでしたか。 今回は約数についてでした。
54と72の公約数は全部で何個ですか?54,72 の因数をすべてまとめ、共通因数を求めます。 54,72 の共通因数は1,2,3,6,9,18 1 , 2 , 3 , 6 , 9 , 18 です。 数因子1,2,3,6,9,18 1 , 2 , 3 , 6 , 9 , 18 の最大公約数(最高公約数)は18 です。
30と18と54の最大公約数はいくつですか?
18,30,54 18 , 30 , 54 の因数をすべてまとめ、共通因数を求めます。 18,30,54 18 , 30 , 54 の共通因数は1,2,3,6 1 , 2 , 3 , 6 です。 数因子1,2,3,6 1 , 2 , 3 , 6 の最大公約数(最高公約数)は6 です。
性質 216は合成数であり、約数は1, 2, 3, 4, 6, 8, 9, 12, 18, 24, 27, 36, 54, 72, 108, 216である。 約数の和は600。つまり、540の約数は2、2、3、3、3、5のかけ算で作られているのです。 これが約数の構造といえます。 この構造を念頭に、約数を規則正しく、過不足なく書き出していきます。 よって24個となります。性質 525は合成数であり、約数は 1, 3, 5, 7, 15, 21, 25, 35, 75, 105, 175, 525 である。