ニュース 有効桁の考え方は?. トピックに関する記事 – 有効数字はどこまでが正しい数字ですか?
今回はそもそも有効数字とは何かについて軽く触れておきます。 有効数字とは「どこまでが正しいのかを表す数」です。 定規やメスシリンダーなどで目盛りを読み取るときは目盛りの10分の1まで読むことが決まりになっています。小数点より右にある0は有効数字です。 例えば,12.00は有効数字4桁です。例えば,0.012345は有効数字5桁,0.012は有効数字2桁,0.0001は有効数字1桁です。
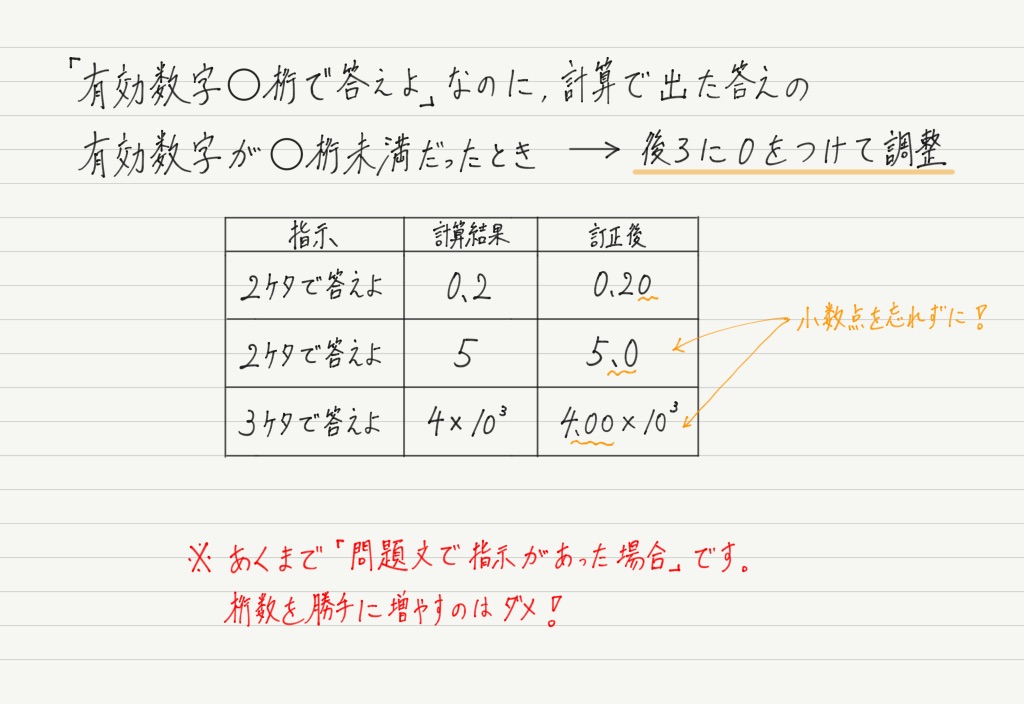
有効桁数の表記方法は?有効数字は科学表記で書く。 例えば 1 より小さい数で、3 桁の有効数字の結果を 0.0000543 等と書くと わかりにくいので、5.43×10-5 とすると、有効桁を明示することができる。 反対に 5.43×105 (有効数字 3 桁) を 543000(有効数字 5 桁)などと書いてはいけない。
有効数字をはっきりさせた表し方は?
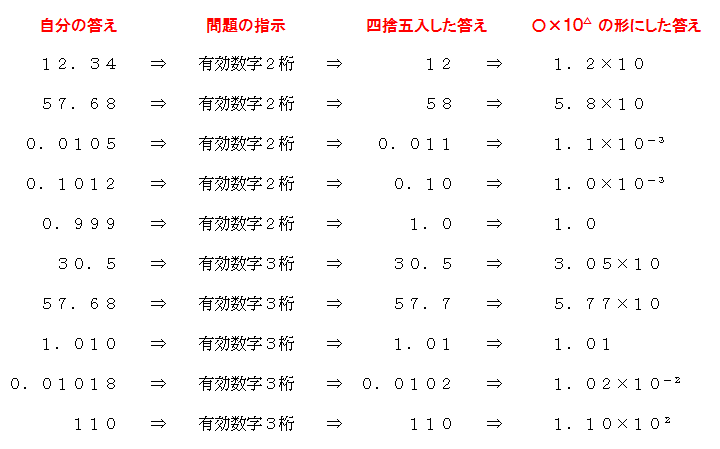
測定値について、どこまでが有効数字で あるかをはっきりさせたいときは、(整数部分が 1 けたの数)×(10 の累乗)の形に表すことがある。数をアラビア数字で書いて表すとき、1~9の数字並びの前後にある0を除き、途中の0はそのままとし、残る数字並びが有効数字(significant figures) です。 大きな整数で、有効数字の後ろに0が続くとき、どこまでの0が意味を持つか、つまり、0を有効数字とする境界,が曖昧になります。
有効数字とは 何桁?
数をアラビア数字で書いて表すとき、1~9の数字並びの前後にある0を除き、途中の0はそのままとし、残る数字並びが有効数字(significant figures) です。 大きな整数で、有効数字の後ろに0が続くとき、どこまでの0が意味を持つか、つまり、0を有効数字とする境界,が曖昧になります。
数値計算や測定値の扱いなどで用いられる用語。 その場合,与えられた数値は誤差を伴っている。 したがって,その誤差の限界に応じて,その数値がどの桁まで信頼できるかがきまってくる。
有効数字とはどっちに合わせる?
与えられた数値の有効数字の桁数はどちらも2桁なので,「割り算の計算結果を,有効数字の桁数が小さい方の数値の桁数にあわせる」と,答えの有効数字の桁数は2桁になることがわかります。例えば、5.00の有効桁数は3です。 実数は、有効数字と有効桁数とが分かる表記法を使います。 例えば、1×103や 1.e3 は有効数字が1桁であり、1.000×103 は4桁であると明示できます。小数第 2 位の数字が 5 以外のときは通常の四捨五入。 小数第 2 位の数字が 5 の場合、小数第 3 位以下の数値が 0 でなければ、切り上げ。
和と差の場合は、桁ではなく位で有効数字を合わせる。 小数第 位までどうしの和と差は、小数第 位までと する。 有効数字が異なるときは、小さい方をとる。 (例) ・長さ と の和は、有効数字は小数第2位までで とする。
有効数字を4桁に丸めるには?有効桁数 4 桁に丸める、という場合は上で示した桁数だけが残るよ うに、ルールに従って数値を丸めます。 例えば 10.256 や 10.400 や 10.496 を整数に丸めるなら切り 捨てて 10。 10.600 や 10.612 や 10.892 なら切り上げて 11。
有効数字の桁数はどちらに合わせる?与えられた数値の有効数字の桁数はどちらも2桁なので,「割り算の計算結果を,有効数字の桁数が小さい方の数値の桁数にあわせる」と,答えの有効数字の桁数は2桁になることがわかります。
3.0+ 2の有効数字はいくつですか?
「3.0 + 2」の場合、答えは「5」で有効数字は1桁です。 足し算では、答えの有効数字は有効数字が一番少ないものになります。 掛け算や割り算でも同様です。
一般に小数点より左側に一桁だけ数字が出るようにしてそれ以下の桁の数値を小数点以下に持って行き、絶対的な大きさを 10X の指数表現で表すようにする。 そうすると有効桁数は小数点以下の数値の並びの個数から、また絶対的な大きさは指数xの値から直ちに読み取ることができる。最もよく使われているパスワード2021年版、「qwerty」など依然上位に
- 123456(1億317万552件)
- 123456789(4602万7530件)
- 12345(3295万5431件)
- qwerty(2231万7280件)
- password(2095万8297件)
- 12345678(1474万5771件)
4桁の数字並びは10,000通りあるので、最長10,000秒(2時間46分40秒)かかるので、若干強度があがるように感じるが、物理的に数字を回すかわりにデジタル技術で総当り攻撃されると100秒かからず解除されてしまう(1処理0.01秒換算)。