ニュース 危険水準とは何ですか？. トピックに関する記事 – 「危険率5%」とはどういう意味ですか？

ここで いう 「危険率5%」 とは、 100回に5回は偶然 に起こるという意味であり、危険率を有意水準 ともよぶ。［意味］ 物事が不安定になり、危機に陥るおそれのある状況のたとえ。 世論調査の内閣支持率は20％台が「危険水域」とされ、20％を切ると「退陣」などともいわれる。有意水準（危険率） 「棄却されるかどうか」の判断基準は帰無仮説が成立する確率を指標とする。 この確率を有意水準（もしくは危険率）と呼ぶ。 有意水準の設定に明確な基準はないが，一般的には5% (0.05)か1% (0.01)が採用されることが多い。

有意水準5%はなぜ5%なのでしょうか？有意水準5%が最初に提唱されたのは？ 実は有意水準の5%に合理的な理由がある訳ではなく、R.A. Fisherという人が最初にそれを提唱したからです。 その理由は、「5%に該当する標準正規分布の棄却限界値が約2で便利だから」というものです（正規分布は別記事で説明します）1。

有意水準と危険度の関係は？

有意水準とは危険率とも呼ばれ逆に100%から危険率を引いた値を信頼率と呼びます。 例えば『有意水準5%』であれば信頼率は95%です。 有意水準(危険率)の意味ですが、これが5%なら5%の確率で判定を誤るリスクがある事で、逆を表す信頼率は95%の確率で信頼できる事になります。用語：p値と危険率

「偶然でt値が2.59を超える確率」のことをp値と呼びます。 p値が0.05（5%）を下回れば、有意差ありとみなすのが、統計学の伝統です。 この5％の基準のことを危険率と呼びます。

1パーセントの有意水準とはどういう意味ですか？

有意水準１％ということは、帰無仮説を棄却する可能性が 1％であることを さします。 言い換えれば、99％の信頼度（もしくは信頼係数）で仮説を検 定しているのです。

統計量の実現値においてP値が0.05（5％）以下ということは、「帰無仮説が正であれば（つまり仮説が成立しない）、観測されたような事象が生じる確率は5%以下と極めて珍しい。 従って帰無仮説は成り立ちにくく、仮説が正である可能性が高い」ということです。

有意水準5%で棄却されるのは？

有意水準5%では、p値が0.05より小さいため(0.04<5%)、帰無仮説は棄却され、有意な結果となります（対立仮説が証明される）。 検定統計量が「臨界値」より「大きい」ことは、P値が有意水準より「小さい」ことを意味します。 つまりこの時、帰無仮説は棄却されます。有意性の判定基準として通常は「P値（有意確率）」が使われており、調査・研究対象によって違いはありますが、一般的には0.05（= 5%）を有意水準として、P値が0.05以下の時に仮説が有意であるとされます。有意水準１％ということは、帰無仮説を棄却する可能性が 1％であることを さします。 言い換えれば、99％の信頼度（もしくは信頼係数）で仮説を検 定しているのです。

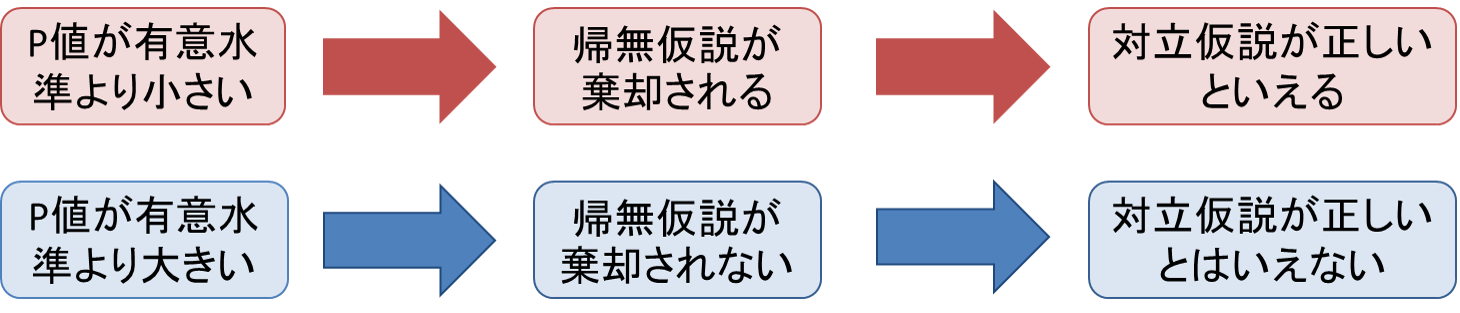
高いp値：データの帰無が真である可能性が高いです。 低いp値：データの帰無が真である可能性は低いです。

P値はどのくらいで有意水準ですか？有意性の判定基準として通常は「P値（有意確率）」が使われており、調査・研究対象によって違いはありますが、一般的には0.05（= 5%）を有意水準として、P値が0.05以下の時に仮説が有意であるとされます。

有意水準はどこからどこまでが有意水準ですか？研究の世界では統計的な有意性が求められます。 有意性の判定基準として通常は「P値（有意確率）」が使われており、調査・研究対象によって違いはありますが、一般的には0.05（= 5%）を有意水準として、P値が0.05以下の時に仮説が有意であるとされます。

有意水準の5%と1%の違いは何ですか？

有意水準とは、有意水準とは、有意差検定を行う際に、帰無仮説を棄却する基準のことです。 1％、5％、10％が用いられます。 1％は5％に比べ厳密であり有意差が出にくい。 一方10％は、5％に比べ有意差が出やすくなります。

P値とは、特定の値になる確率ではなく、それよりも大きくなる確率（実測された差よりも大きな差になる確率）です。 その値が小さければ、実測された差よりも大きくなる確率はめったにないため、仮説が棄却されます。P値が小さいほど、検定統計量がその値となることはあまり起こりえないことを意味する。 一般的にP値が5％または1％以下の場合に帰無仮説を偽として棄却し、対立仮説を採択する。有意水準が大きくなる（第一種の過誤確率が高くなる、基準の甘い判定）と、帰無仮説を否定しやすくなるため検出力は上がります。 またサンプルサイズが大きくなると、推定のばらつきが小さくなることを通して、検出力が高くなります。 データのばらつきが小さいことも、推定のばらつきが小さくなることに直結するので同様です。